21.03.2013
JavaFX - Mandelbrot Set
The following article describes how to paint a Mandelbrot set with JavaFX. The Mandelbrot set will be painted into a javafx.scene.canvas.Canvas with the methods GraphicsContext.setFill() and GraphicsContext.fillRect().
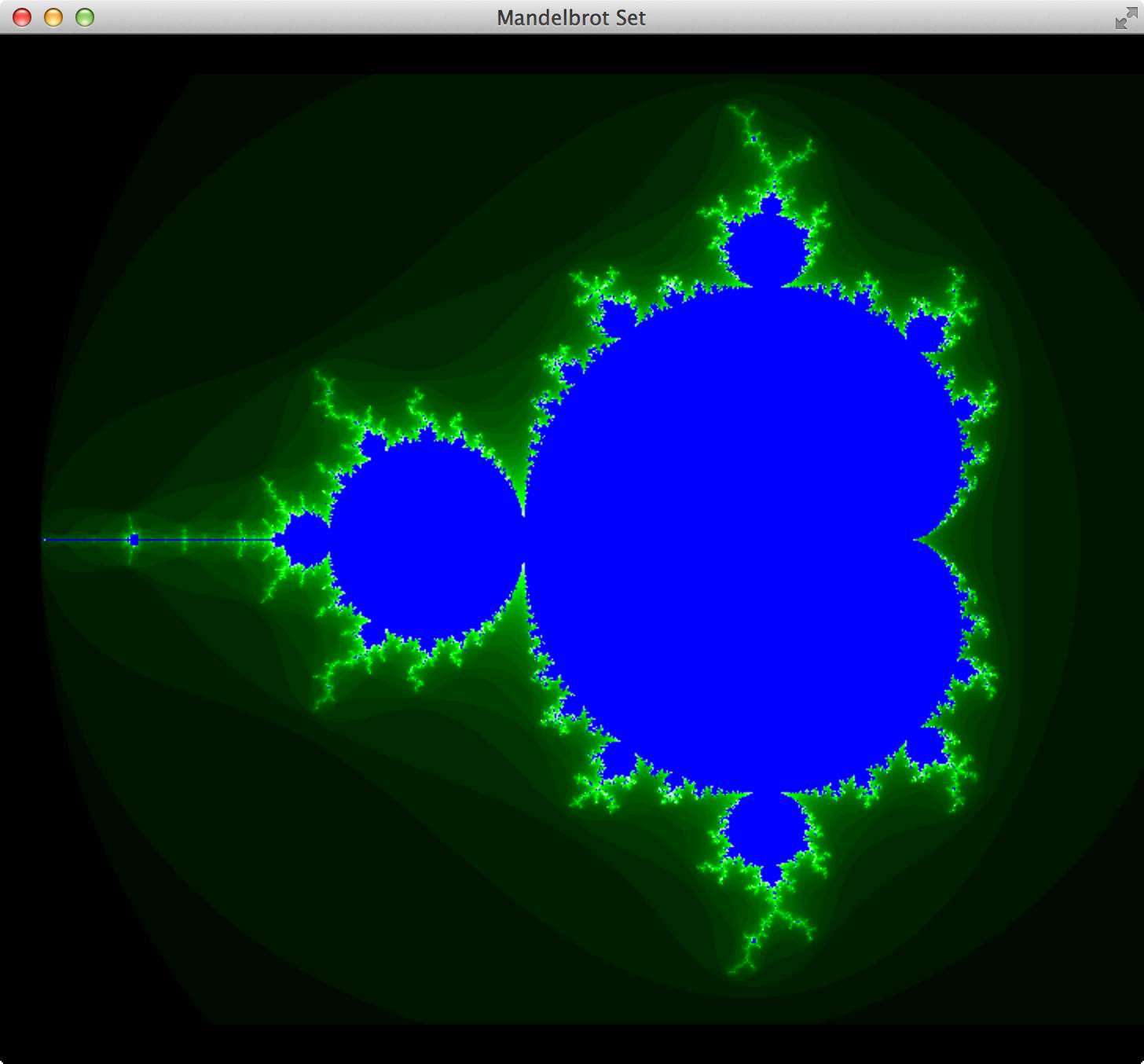
The algorithm to calculate the color of the points of the Mandelbrot set is very simple. The Mandelbrot set is a set of points in a two-dimensional system. The Mandelbrot set is defined through the recursive definition z(n+1) = z(n)^2 + c where z(n) and c are complex numbers. The start value of z(0) is 0. The interesting points of the Mandelbrot set are between z = {-2..1} and zi = {-1..1}. (Note: z(n) = z + zi)
To generate a graphical representation of the Mandelbrot set you calculate the speed of the convergence (convergenceValue) of every point in the set. The convergenceValue is mapped to a color. So every point in the set has a color and the result is a graphical representation of the Mandelbrot set.
package org.hameister.javafx.mandelbrotset;
import javafx.application.Application;
import javafx.scene.Scene;
import javafx.scene.canvas.Canvas;
import javafx.scene.canvas.CanvasBuilder;
import javafx.scene.canvas.GraphicsContext;
import javafx.scene.layout.Pane;
import javafx.scene.paint.Color;
import javafx.stage.Stage;
/**
* Mandelbrot set with JavaFX.
* @author hameister
*/
public class JavaFXMandelbrotSet extends Application {
// Size of the canvas for the Mandelbrot set
private static final int CANVAS_WIDTH = 740;
private static final int CANVAS_HEIGHT = 605;
// Left and right border
private static final int X_OFFSET = 25;
// Top and Bottom border
private static final int Y_OFFSET = 25;
// Values for the Mandelbro set
private static double MANDELBROT_RE_MIN = -2;
private static double MANDELBROT_RE_MAX = 1;
private static double MANDELBROT_IM_MIN = -1.2;
private static double MANDELBROT_IM_MAX = 1.2;
@Override
public void start(Stage primaryStage) {
Pane fractalRootPane = new Pane();
Canvas canvas = CanvasBuilder
.create()
.height(CANVAS_HEIGHT)
.width(CANVAS_WIDTH)
.layoutX(X_OFFSET)
.layoutY(Y_OFFSET)
.build();
paintSet(canvas.getGraphicsContext2D(),
MANDELBROT_RE_MIN,
MANDELBROT_RE_MAX,
MANDELBROT_IM_MIN,
MANDELBROT_IM_MAX);
fractalRootPane.getChildren().add(canvas);
Scene scene = new Scene(fractalRootPane, CANVAS_WIDTH + 2 * X_OFFSET, CANVAS_HEIGHT + 2 * Y_OFFSET);
scene.setFill(Color.BLACK);
primaryStage.setTitle("Mandelbrot Set");
primaryStage.setScene(scene);
primaryStage.show();
}
private void paintSet(GraphicsContext ctx, double reMin, double reMax, double imMin, double imMax) {
double precision = Math.max((reMax - reMin) / CANVAS_WIDTH, (imMax - imMin) / CANVAS_HEIGHT);
int convergenceSteps = 50;
for (double c = reMin, xR = 0; xR < CANVAS_WIDTH; c = c + precision, xR++) {
for (double ci = imMin, yR = 0; yR < CANVAS_HEIGHT; ci = ci + precision, yR++) {
double convergenceValue = checkConvergence(ci, c, convergenceSteps);
double t1 = (double) convergenceValue / convergenceSteps;
double c1 = Math.min(255 * 2 * t1, 255);
double c2 = Math.max(255 * (2 * t1 - 1), 0);
if (convergenceValue != convergenceSteps) {
ctx.setFill(Color.color(c2 / 255.0, c1 / 255.0, c2 / 255.0));
} else {
ctx.setFill(Color.PURPLE); // Convergence Color
}
ctx.fillRect(xR, yR, 1, 1);
}
}
}
/**
* Checks the convergence of a coordinate (c, ci) The convergence factor
* determines the color of the point.
*/
private int checkConvergence(double ci, double c, int convergenceSteps) {
double z = 0;
double zi = 0;
for (int i = 0; i < convergenceSteps; i++) {
double ziT = 2 * (z * zi);
double zT = z * z - (zi * zi);
z = zT + c;
zi = ziT + ci;
if (z * z + zi * zi >= 4.0) {
return i;
}
}
return convergenceSteps;
}
public static void main(String[] args) {
launch(args);
}
}
In the start method you create a Pane and add the Canvas for the Mandelbrot set. The Pane is part of the Scene. The variables X_OFFSET and Y_OFFSET are used to create space between the border and the canvas.
The paintSet method is used to examine all points of the Mandelbrot set. For every point the convergence is checked with the method checkConvergence. The convergenceValue is used to create a Color which is used to fill a rectangle with the size 1. If a point is convergent a pre-defined color is used (Color.PURPLE).
The interesting part of the application is the method checkConvergence. In this method the complex number c(n) = ci + c is analyzed. The lines 84 and 85 calculate (zi+z)^2 = (xi)^2 + 2(zi+z) + z^2. Please note i^2=-1. So you get 2*(z+zi) and z*z - zi*zi. In the lines 86 and 87 the real and imaginary part of number c is added to z. The if-statement is used to check if the number converged. The condition is a simplification of |x|>2. If z is greater that 2 the function diverges very fast so you can leave the method with return. The number of needed steps i are the convergenceValue. The variable convergenceSteps is needed to interrupt the loop for the divergent numbers.
More informations about the Mandelbrot set can be found here.
I extended this simple application so it is possible to display the Julia set, too. Also it is possible to change the colors of the set. Here you can see a video preview of the application:
The article how to create such an application can be found here: JavaFX - Fractal: The Mandelbrot and the Julia Set.

