25.06.2008
Zeichnen von Punkten mit Objective-C und Cocoa
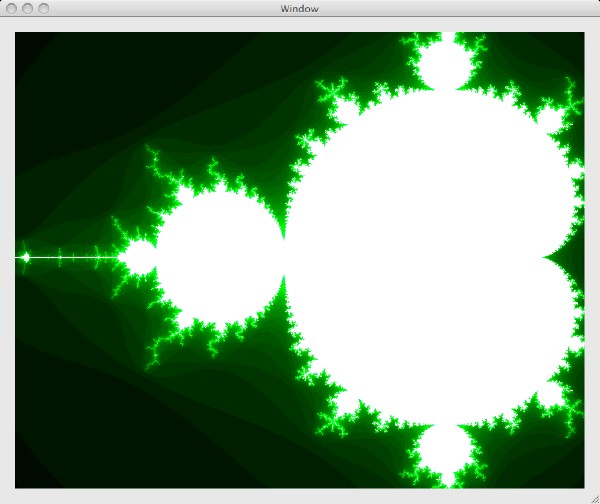
Hier werden zwei Möglichkeiten zum Zeichnen von Punkten in Cocoa vorgestellt. Eine Methode, die mit Hilfe von Bezierkurven arbeitet und eine Methode, die mit NSRectFill einen Punkt zeichnet. In dem Beispiel wird ein einfaches Apfelmännchen gezeichnet.
Der Begriff Fraktal wurde von Benoit Mandelbrot geprägt und ist durch das "Apfelmännchen" berühmt geworden. Interessant an der Sache ist die recht einfach aussehende Definition der Mandelbrotmenge, deren grafische Darstellung das "Apfelmännchen" ergibt.
Definiert wird die Mandelbrotmenge M über die Menge der komplexen Zahlen c, z(i) und der rekursiven Definition: z(n+1)= z(n)^2+c, wobei der Anfangswert z(0)=0 ist. Zu der grafischen Darstellung der Menge kommt man, indem man die Konvergenz der einzelnen Werte der Menge untersucht und für den Grad der Konvergenz eine Farbe aufträgt.
Erstaunlich ist, daß mit einem sehr kleinen Code-Schnipsel der Grad der Konvergenz und damit die Mandelbrot-Menge berechnet werden kann.
Die folgende Funktion berechnet die Konvergenz.
int checkFast(double ci, double c) {
double zi = 0;
double z = 0;
int i = 0;
int deep = 50;
for(i=0;i<deep;i++) {
double ziT = 2*(z*zi);
double zT =z*z-(zi*zi);
z = zT + c;
zi = ziT + ci;
if(z*z + zi*zi >= 4.0) {
return i;
}
}
return deep;
}
Zu beachten sind die Zeilen 6 und 7. Dort werden die Rechenregeln für die komplexen Zahlen umgesetzt. D.h. (zi+z)^2 = (xi)^2 + 2(zi+z) + z^2. Wobei ja gilt i^2=-1. Also erhält man: 2*(z+zi) und z*z - zi*zi. Die Ergebnisse der Rechnung werden in temporären Variablen gehalten (Es hätte auch eine Variable ausgereicht). In den Zeilen 8 und 9 wird der reelle und imaginäre Anteil jeweils addiert, wie in der rekursiven Definition festgelegt. deep gibt an, bis zur welcher Tiefe die Folge auf Konvergenz untersucht werden soll.
Besonders interessant ist die Abbruchbedingung in Zeile 10. Es wird davon ausgegangen, daß eine Folge divergiert, wenn das Quadrat des Betrags von z(n) größer als 4 ist.
Die folgende Funktion zeichnet den Hintergrund und den Rahmen der Anwendung. Durch den Aufruf der Funktion createRect wird das Apfelmännchen gezeichnet.
- (void)drawRect:(NSRect)rect {
NSRect gridRect;
// Hintergrund und Rahmen zeichnen
[[NSColor blackColor] set];
NSEraseRect( rect );
NSFrameRect( [self bounds] );
[[NSGraphicsContext currentContext] setShouldAntialias:NO];
[self createRect:gridRect] ;
}
Folgende Funktion zeichnet das Fraktal:
- (void) createRect:(NSRect)gridRect {
double gran = 0.003;
int xStart = 600;
int xEnd = 150;
int yStart =300;
int yEnd = 300;
int points[xStart+xEnd][yStart+yEnd];
int x;
int y;
int xR;
int yR;
for(x=-xStart, xR=0;x<xEnd;x++,xR++) {
for(y=-yStart, yR=0;y<yEnd;y++,yR++) {
points[x+xStart][y+yStart] = checkFast(y*gran,x*gran);
double t1=(double)points[xR][yR] / 50;
int c1=fmin(255*2*t1,255);
int c2=fmax(255*(2*t1-1),0);
[[NSColor colorWithCalibratedRed:((float)c2)/255.0 green:(float)c1/255.0 blue:(float)c2/255.0 alpha:0.8] set];
NSBezierPath* grid = [NSBezierPath bezierPath];
[grid setLineWidth:1.0];
[grid moveToPoint:NSMakePoint(xR, yR)];
[grid lineToPoint:NSMakePoint(xR+1, yR)];
[grid stroke];
}
}
}
Das Fraktal soll eine Größe von 750x600 Pixeln haben. Deshalb wird ein zweidimensionales Array mit int-Werten initialisiert. In den zwei for-Schleifen wird zuerst der Grad der Konvergenz mit der Funktion checkFast berechnet und das Ergebnis gespeichert. Anhand dieses Wertes wird eine Farbverteilung berechnet und daraus ein Objekt von Type NSColor erstellt. Im Anschluß wird mit einer Bezierkurve ein Punkt gezeichnet. Dazu wird mit der Funktion moveToPoint der Cursor zum Startpunkt bewegt und mit der Funktion lineToPoint von dort eine Linie der Länge 1 gezeichnet. Wie man sich leicht vorstellen kann, ist dies nicht der optimale Weg. Diese Methode ist recht langsam. Deshalb wird mit folgenden Beispiel eine andere Methode vorgestellt, die schneller ist.
- (void) createRect:(NSRect)gridRect {
double gran = 0.003;
int xStart = 600;
int xEnd = 150;
int yStart =300;
int yEnd = 300;
int points[xStart+xEnd][yStart+yEnd];
int x;
int y;
int xR;
int yR;
for(x=-xStart, xR=0;x<xEnd;x++,xR++) {
for(y=-yStart, yR=0;y<yEnd;y++,yR++) {
points[x+xStart][y+yStart] = checkFast(y*gran,x*gran);
double t1=(double)points[xR][yR] / 50;
int c1=fmin(255*2*t1,255);
int c2=fmax(255*(2*t1-1),0);
[[NSColor colorWithCalibratedRed:((float)c2)/255.0 green:(float)c1/255.0 blue:(float)c2/255.0 alpha:1] set];
NSRectFill(NSMakeRect(xR,yR,1,1));
}
}
}
Zu dem vorherigen Beispiel gibt es nur den Unterschied, daß die Funktion NSRectFill verwendet wird um eine Rechteck der Länge 1 zu zeichnen. Diese Methode ist erheblich schneller als die Bezier-Kurve.
Um die Code-Schnipsel in eine Applikation einzubauen, legt man ein neues Projekt an und verwendet das Template für eine Cocoa-Application.
Die oben aufgeführten Code-Schnipsel packt man am besten in eine Klasse FractalView, die von NSView erbt.
Die Header-Datei sieht folgendermaßen aus:
#import <Cocoa/Cocoa.h>
#import <Math.h>
@interface FractalView : NSView
{
}
@end
Hier die passende Implementierung:
#import "FractalView.h"
@implementation FractalView
- (void) createRect:(NSRect)gridRect {
...
}
int checkFast(double ci, double c) {
...
}
- (void)drawRect:(NSRect)rect {
...
}
@end
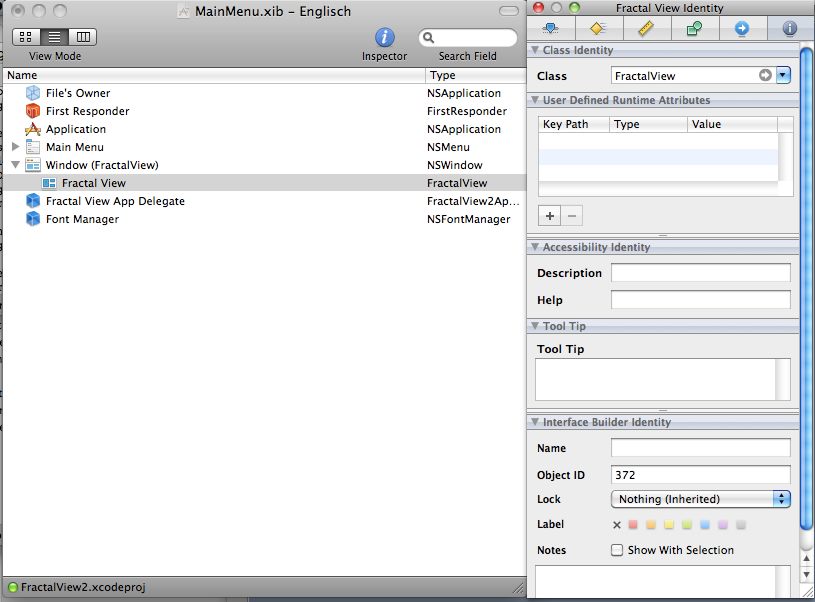
Nach einem Doppelklick auf die Datei MainMenu.xib in Xcode öffnet sich der Interface Builder. Dort klappt man Window auf, startet den Inspector und selektiert das Tab Identity. Unter class wird FractalView eingetragen.
Wenn man das Programm nach dem Speichern und Builden startet, dann sollte folgendes Bild entstehen: